Recursive linear polymer generation with Lpr
The Lpr class in the pysoftk.linear_polymer.linear_polymer module provides a powerful way to generate linear polymers from repeating monomer units. This tutorial will guide you through its usage, explaining the key parameters and options. The Lpr class is initialized with a starting SMILES string, a dictionary of replacements, and the maximum number of repetitions.
Let’s start with a simple example of generating polystyrene.
from pysoftk.linear_polymer.linear_polymer import Lpr
smiles = "CC(c1ccccc1){R}"
replacements = {"R": "CC(c1ccccc1){R}"}
final_replacement = ""
lpr_instance = Lpr(smiles, replacements, max_repetitions=10, final_replacement=final_replacement)
result = lpr_instance.generate_recursive_smiles(force_field="MMFF", relax_iterations=250, rot_steps=1)
print(result)
This is the result of the recursive implementation:
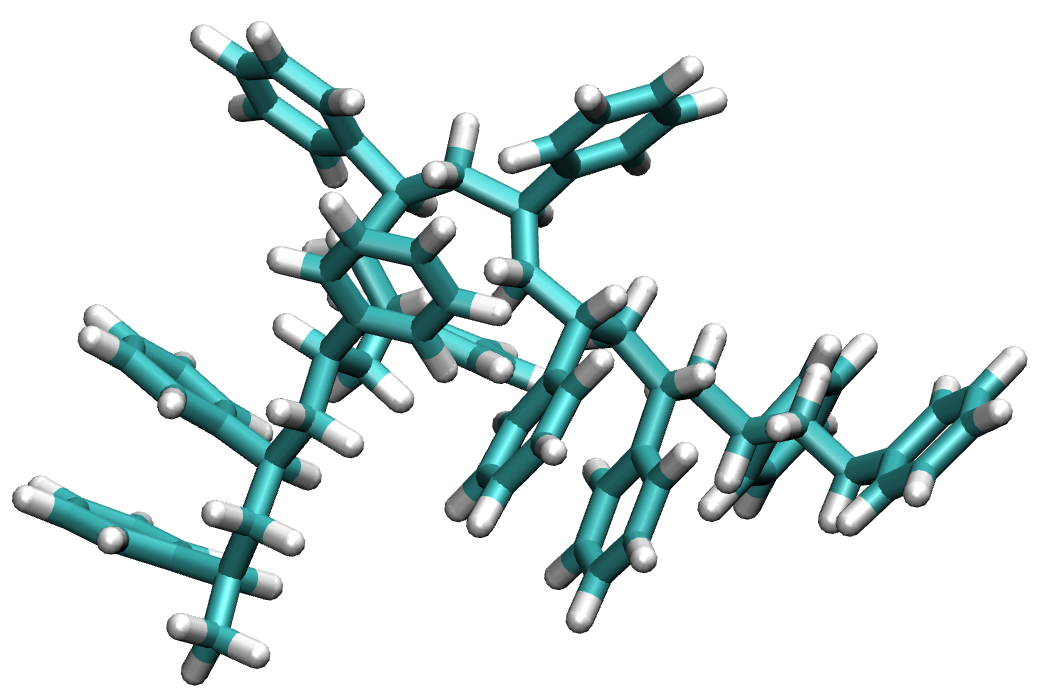
Figure recursive linear polymer with 10 styrene units.
Initialization: *
smiles = "CC(c1ccccc1){R}": This is the starting SMILES string. The{R}placeholder indicates the point where the polymer chain will extend. *replacements = {"R": "CC(c1ccccc1){R}"}: This dictionary defines the replacement rule. The{R}placeholder in the replacement string is crucial for recursive polymer growth. *max_repetitions=10: This specifies the number of times the replacement rule will be applied, determining the polymer’s length. *final_replacement = "": This allows a final modification to the end of the polymer chain. In this case, there’s no final replacement. *lpr_instance = Lpr(smiles, replacements, max_repetitions=10, final_replacement=final_replacement): This creates an instance of the Lpr class.Polymer Generation: *
result = lpr_instance.generate_recursive_smiles(force_field="MMFF", relax_iterations=250, rot_steps=1): This generates the polymer using the specified parameters. *force_field="MMFF": Specifies the force field to use for geometry optimization. *relax_iterations=250: Sets the number of iterations for geometry optimization. *rot_steps=1: Sets the number of rotational steps. *print(result): Prints the generated molecule.
Lpr Class Parameters
The Lpr class contains the following parameters:
`smiles` (str): The starting SMILES string.
`replacements` (dict): A dictionary of replacement rules.
`max_repetitions` (int): The maximum number of repetitions.
`final_replacement` (str, optional): A final replacement string. Defaults to an empty string.
generate_recursive_smiles` Method Parameters
The generative_recursive_smiles function has the following parameters:
`force_field` (str, optional): The force field to use for geometry optimization (e.g., “MMFF”, “UFF”). Defaults to None (no optimization).
`relax_iterations` (int, optional): The number of iterations for geometry optimization. Defaults to 0.
`rot_steps` (int, optional): The number of rotational steps. Defaults to 1.
Further notes:
The
{R}placeholder is essential for defining the polymer chain’s growth points.Geometry optimization can be computationally intensive, especially for large polymers. Adjust
relax_iterationsaccordingly.Ensure that the starting SMILES string and replacement rules are valid.
It is advised to use smaller values for max_repetitions and relax_iterations when testing, and then increase them for the final run.
Here’s an example of generating polyethylene:
from pysoftk.linear_polymer.linear_polymer import Lpr
smiles = "C=C{R}"
replacements = {"R": "C=C{R}"}
final_replacement = ""
lpr_instance = Lpr(smiles, replacements, max_repetitions=20, final_replacement=final_replacement)
result = lpr_instance.generate_recursive_smiles(force_field="MMFF", relax_iterations=250, rot_steps=1)
print(result)
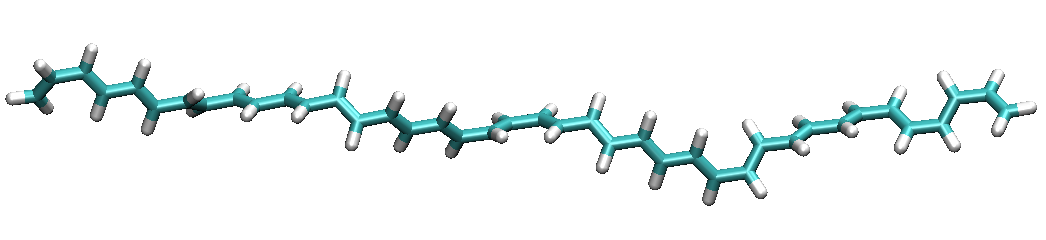
Figure recursive linear polymer with 10 ethylene units.
In this example, we generate a longer polyethylene chain using a higher max_repetitions value. Experiment with different starting SMILES strings and replacement rules to create various linear polymers. Adjust the optimization parameters to fine-tune the resulting structures. This documentation should help you get started with using the Lrp class.