Creating random Polymers
PySoftK supports the construction of random linear copolymers which consist of two or three different monomers. Our approach uses the command Rnp(mol_1,mol_2,atom).random_ab_copolymer(len,pA,iter_ff,FF) to build a random copolymer of length len that contains two monomers, mol_1 and mol_2. The number of mol_1 and mol_2 monomers in the resulting polymer are determined from pA len and (1-pA)len, respectively.
from rdkit import Chem
from rdkit.Chem import AllChem
mol_1=Chem.MolFromSmiles("BrCOCBr")
mol_2=Chem.MolFromSmiles("c1(ccc(cc1)Br)Br")
Then, we can create a polymer with a diblock random topology, by using the following commands:
from pysoftk.topologies.ranpol import *
ran=Rnp(mol_1,mol_2,"Br").random_ab_copolymer(5,0.4,10)
The new molecular unit (stored in the variable ran) can be used to replicate and form a diblock random polymer with a given desired number of units (in total 5). A probability of 0.4 to be merged is defined by the user, while 10 steps for geometry optimization has been requested. The structure can be printed in XYZ format by adding the following lines of code as can be seen in this snipet:
from pysoftk.format_printers.format_mol import *
Fmt(ran).xyz_print("random2.xyz")
By using a common visualization program (such as VMD), the built structure random2.xyz can be displayed and the result as presented above
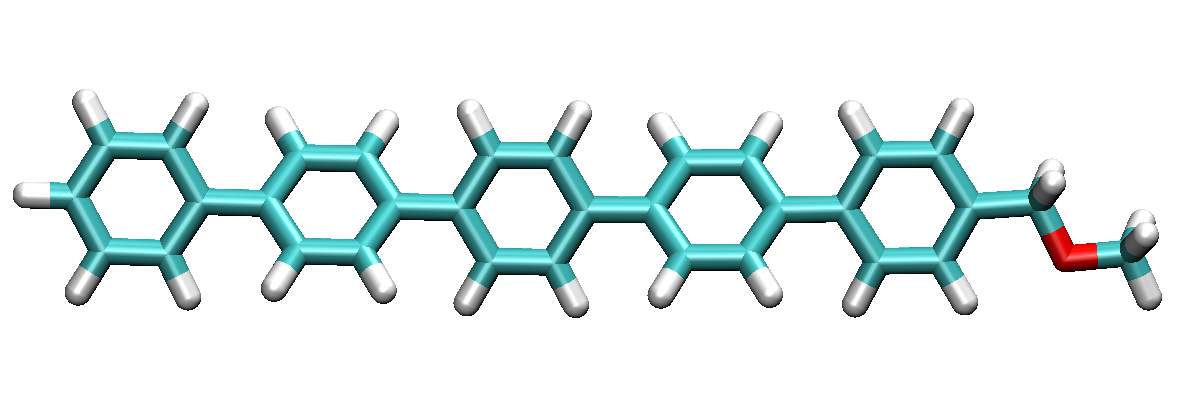
Figure Random diblock polymer with 5 units.
Similarly PySoftK can be used to generate random linear copolymers consisting of three different monomers via the command Rnp(mol_1,mol_2,atom).random_abc_copolymer(mol_3, len, pA, pB, iter_ff, FF). In this case, the resulting polymer will contain len monomers, such that the number of mol_1, mol_2 and mol_3 monomer is pA len, pB len and (1-pA-pB) len, respectively
from pysoftk.topologies.ranpol import *
mol_3=Chem.MolFromSmiles("c1cc(oc1Br)Br")
tri=Rnp(mol_1,mol_2,"Br").random_abc_copolymer(mol_3,5,0.4,0.2,10)
Fmt(tri).xyz_print("random3.xyz")
The result of this function is displayed in the figure below.
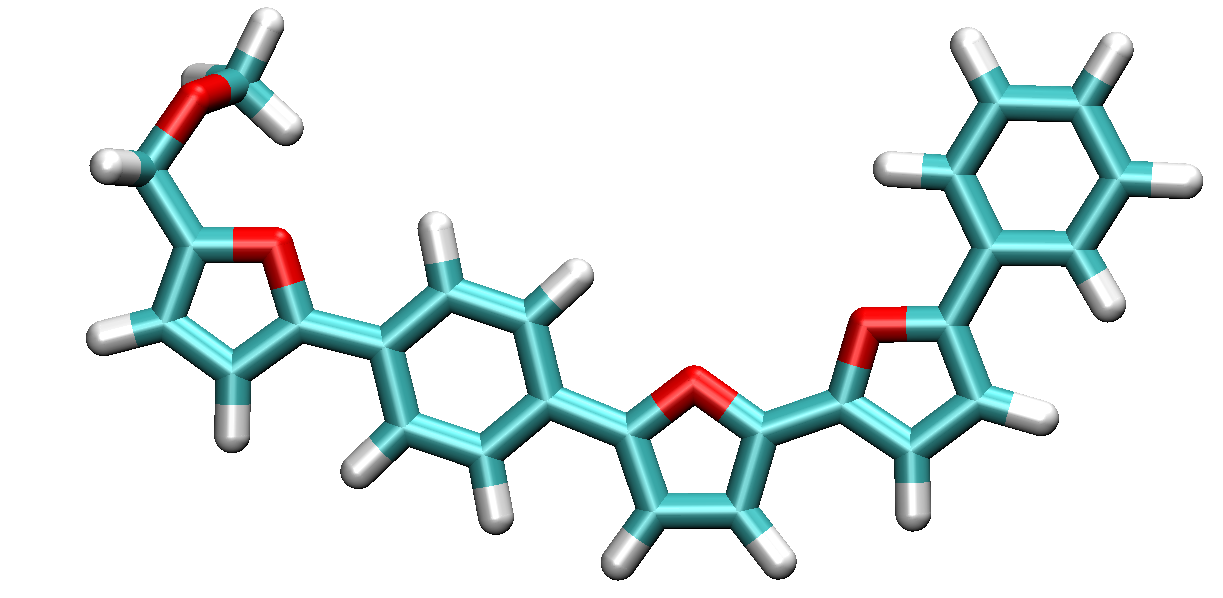
Figure Random triblock 5-unit repetition polymer